LTI System
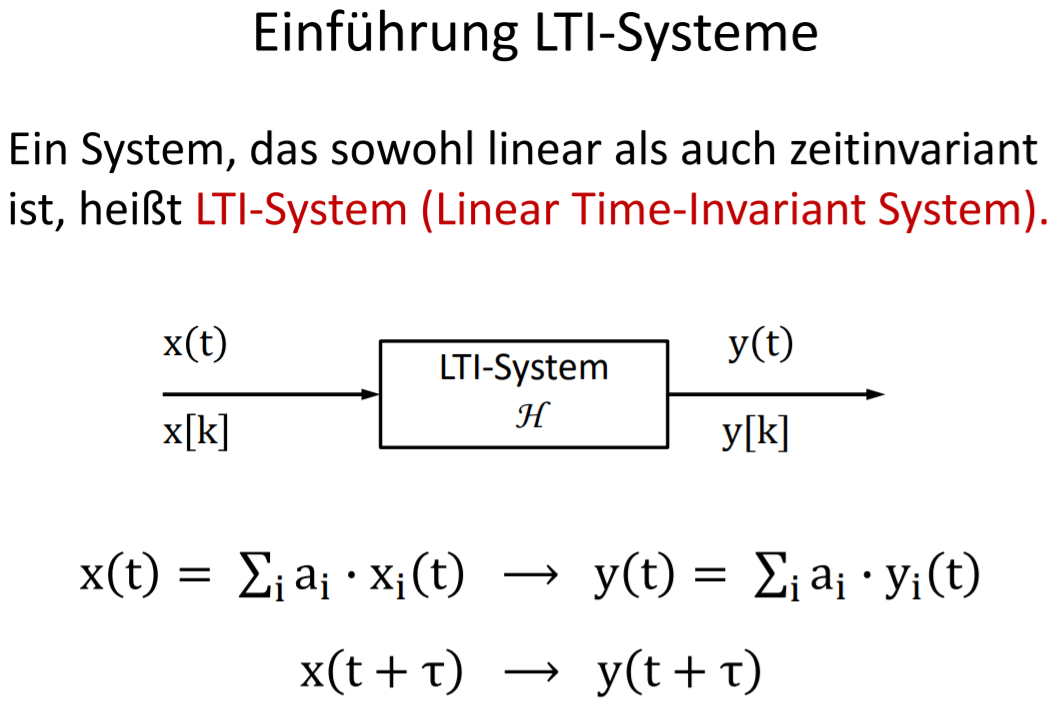
LTI-Systeme haben eine herausragende Bedeutung in der Signal- und Systemanalyse.
Warum?
Linearität und Zeitinvarianz erlauben eine effiziente und relativ einfache Beschreibung und Berechnung des Systemverhaltens.
LTI-Systeme haben besondere Eigenschaften: Regt man ein LTI-System mit einer harmonischen Schwingung der Frequenz 𝑓 an, so kann es nur mit einer harmonischen Schwingung derselben
Frequenz 𝑓 antworten. -> LTI-Systeme können keine neuen Frequenzen erzeugen! Denn lineare Abbildungen modifizieren nicht die Frequenz harmonischer Signale!
Anwendung:
1. Zerlegung eines komplizierten Eingangssignals in seine harmonischen Anteile
2. Berechnung der Systemantworten des linearen Systems für jeden Anteil separat
LTI-Systeme können gleichwertig im Zeit- und im Bildbereich beschrieben werden: Zeitbereich 1. lineare Differential-/Differenzengleichungen 2. Impuls- und Sprungantwort/ Bildbereich 3. Übertragungsfunktion 4. Frequenzgang
3 Erkenntnis (Möglichkeiten Systemantwort bestimmen)
-Statische LTI-Systeme (diskret und analog) lassen sich im Zeitbereich durch algebraische Gleichungen beschreiben.
-Diskrete LTI-Systeme lassen sich durch lineare Differenzengleichungen mit konstanten und reellen Koeffizienten beschreiben. Damit ist eine Simulation des Systemverhaltens möglich.
-Kontinuierliche LTI-Systeme lassen sich durch lineare Differentialgleichungen mit konstanten und reellen Koeffizienten beschreiben. Diese lassen sich nicht immer einfach lösen.
Definition: Impulsantwort wird ein energiefreies LTI-System mit einem Dirac-Impuls angeregt, so nennt man die Antwort des Systems Impulsantwort g (t) : δ (t) ⟶ g (t)
Definition: Sprungantwort wird ein energiefreies LTI-System mit einem Einheitssprung angeregt, so nennt man die Antwort des Systems Sprungantwort h (t) : σ (𝑡) ⟶ h (t)
Impuls- und Sprungantwort
Ein LTI-System kann mit Hilfe der Impulsantwort oder der Sprungantwort vollständig beschrieben werden.
Man erhält die Impulsantwort durch Anregung des Systems mit einem Dirac-Impuls.
Man erhält die Sprungantwort durch Anregung des Systems mit der Sprungfunktion.
Für theoretische Untersuchungen ist die Impulsantwort vorteilhaft wegen ihrer mathematischen Eigenschaften (z.B. FT δ t = 1).
Die Sprungantwort ist technisch besser realisierbar und wird deshalb v.a. in der Elektro-, Mess- und Regelungstechnik häufiger verwendet.
Die Impulsantwort kann durch Differenzieren aus der Sprungantwort berechnet werden.
Bạn đang đọc truyện trên: TruyenTop.Vip